Cos'è il suono

-> Acustica -> Cos'è il suono

Come tutti i fenomeni fisici che interessano i nostri sensi, il suono è un argomento complesso da trattare perchè richiede sia una trattazione fisica oggettiva (nella quale il suono è un fenomeno ondulatorio in un mezzo elastico) sia una trattazione che tenga conto della nostra percezione (nella quale si intende il suono come fenomeno soggettivo a seconda di chi ne viene investito); nei due casi si parlerà di acustica o di psicoacustica.
Nel seguito e nei prossimi tutorial dichiareremo preventivamente se stiamo affrontando il punto di vista acustico o quello psicoacustico.

In questo tutorial affronteremo, per ora solo dal punto di vista strettamente fisico, una panoramica sui fenomeni sonori, cercando di coniugare il più possibile la semplicità nell'esposizione con una certa rigorosità.

Allora, dal punto di vista fisico, cos'è il suono?
Il suono giunge all'orecchio umano come variazione della pressione atmosferica.
Ogni variazione (purchè sia sufficientemente grande, e poi vedremo cosa questo voglia dire) produce nel nostro orecchio una reazione che genera ciò che noi chiamiamo un suono.
Queste variazioni sono comunque molto piccole rispetto alla pressione atmosferica, e difatti non sono misurabili con un comune barometro.
Le variazioni sono dette onde di pressione sonora. Una visualizzazione classica che aiuta a comprendere cosa può essere un'onda di pressione sonora, è quella delle onde che si producono in una superficie d'acqua quando vi viene gettato un sasso. Ovviamente questa è una situazione che può essere visualizzata in modo bidimensionale, e infatti le onde nell'acqua si possono pensare come cerchi, mentre nel caso delle onde sonore siamo in una situazione tridimensionale, quindi dobbiamo pensare le onde sonore come sferiche.
Per la rappresentazione delle onde sonore è necessaria una certa dose di semplificazione, per poter ridurre casi complessi (interferenze, increspature) a casi più semplici (il caso ideale è quello di un'onda costante che si espande nello spazio libero).

Cominceremo da uno strumento fondamentale per lo studio del suono, la sinusoide semplice, ossia la forma d'onda più semplice possibile.
La rappresentazione sarà bidimensionale - ma non dimentichiamo che in realtà stiamo pensando ad un fenomeno che si sviluppa tridimensionalmente nello spazio.
In modo estremamente generale, possiamo dire che il suono è un fenomeno ondulatorio - che si manifesta in generale in ogni corpo elastico, nella nostra esperienza più comune nell'aria. E' quindi ovvio che nel caso più semplice - oscillazioni costanti nell'ampiezza e nel tempo - la sinusoide sia la migliore rappresentazione di un fenomeno sonoro.
Immaginiamo un esempio molto classico di sinusoide: quello di una penna, solidale ad una massa che oscilla in senso verticale - perchè appesa ad una molla - e di un foglio di carta che scorre in senso orizzontale a velocità costante, come nella figura.
La punta della penna è a contatto del foglio di carta.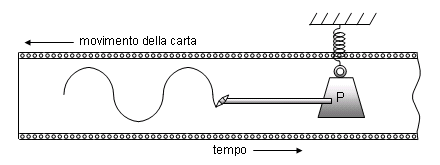

L'immagine che viene disegnata sulla carta dalla penna è una sinusoide.
Si intuisce bene dalla figura quanto la sinusoide sia indicata a descrivere moti oscillatori, infatti il moto della penna è proprio un moto oscillatorio.

Andiamo ora a vedere quali sono i valori che leggeremo sul grafico di un'onda sinusoidale.
Osserviamo la figura: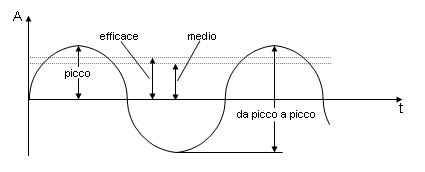

L'asse orizzontale - quello delle ascisse - sarà l'asse del tempo (t), quello sul quale sono segnati gli istanti successivi da sinistra verso destra. l'asse verticale - quello delle ordinate - è quello delle ampiezze (A), dove andremo a leggere l'ampiezza delle oscillazioni.
L'intersezione dei due assi rappresenta, sull'asse delle ascisse, il momento a partire dal quale iniziamo l'osservazione, su quello delle ordinate l'oscillazione nulla.
Il primo valore che notiamo è quello di picco, che rappresenta la massima ampiezza positiva raggiunta sul grafico. Vi è ovviamente anche un valore di picco negativo, che rappresenta la massima ampiezza negativa raggiunta.
Il valore da picco a picco è la differenza tra il valore di picco positivo e quello negativo, ossia la massima oscillazione d'ampiezza.
Il valore medio è la media dei valori assunti dal grafico in un semiperiodo positivo (nella nostra figura, il primo semiperiodo positivo è quello dall'intersezione degli assi alla successiva intersezione della sinusoide con l'asse dei tempi; poi segue un semiperiodo negativo; insieme, semiperiodo positivo e semiperiodo negativo costuiscono un periodo; dopo seguono altri periodi, identici al primo: questo è il motivo per cui la sinusoide è detta un'onda periodica).
Il valore efficace è un valore molto utile nella pratica, in quanto dà una migliore approssimazione, rispetto al valore medio, ovvero fornisce una media significativa dei valori. Per un'onda sinusoidale - e solo in questo caso! - i rapporti tra i vari valori sono restituiti dalle seguenti formule:

Nel caso di un'onda generica, il valore efficace, che viene anche detto RMS (Root Mean Square, "radice delle media dei quadrati"), si ricava suddividendo il grafico in n porzioni uguali sull'asse delle ascisse e ricavando i valori a_n corrispondenti sull'asse delle ordinate, come nella figura seguente (dove per semplicità si è disegnata una sinusoide semplice, ma il caso, ripetiamo, è generale):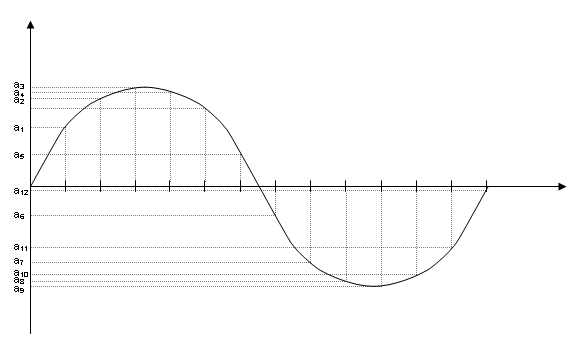

e quindi applicando la formula: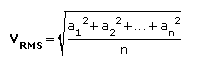

dove, come si vede, viene appunto calcolata la radice delle media dei quadrati dei valori.
Ovviamente, maggiore sarà il numero n delle porzioni in cui viene suddiviso il grafico, migliore sarà l'approssimazione ottenuta. Il valore esatto si ricava col calcolo integrale, che però non è sembrato il caso di introdurre in questa sede.

Abbiamo visto delle esemplificazioni sulle onde di pressione sonora: ora avviciniamoci un po' di più al fenomeno fisico e cerchiamo di comprenderlo un po' meglio.
Immaginiamo alla propagazione del suono nel mezzo che ci è più familiare: l'aria.
Se una particella d'aria viene spostata dalla sua posizione di equilibrio, le forze elastiche tendono a riportarla in tale posizione, appunto, di equilibrio.
Tuttavia, a causa dell'inerzia della particella (quella forza che tende a conservare il moto di un oggetto in movimento), essa si sposta oltre l'originaria posizione di equilibrio, mettendo in azione forze elastiche nella direzione opposta e così via.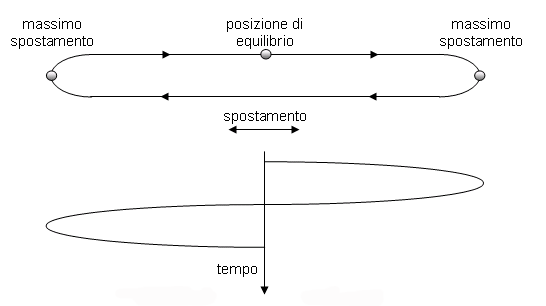

Il suono si propaga nei mezzi elastici, siano essi gas, liquidi o solidi; ad esempio il suono si propaga nell'aria, nell'acqua, nel legno, nell'acciaio, nel cemento.
Senza un mezzo elastico il suono non può propagarsi: nel vuoto dove non c'è alcun mezzo, non può esistere suono.
Il movimento delle particelle d'aria che consentono la propagazione del suono può seguire tre moti diversi: si distinguono onde circolari, onde trasversali e onde longitudinali.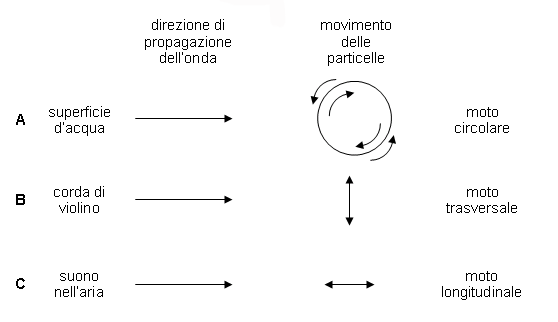

Come possono le particelle d'aria "trasportare" il suono? In realtà il suono non è altro che una "vibrazione" delle particelle d'aria stesse.
osserviamo la prossima figura: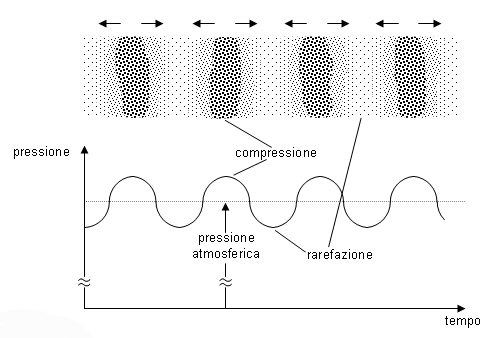

Le molecole più addensate rappresentano le aree di compressione, dove la pressione è lievemente maggiore di quella atmosferica normale. Le aree dove i punti sono più radi rappresentano sacche di rarefazione, dove la pressione è leggermente inferiore a quella atmosferica. Le molecole tenderanno a muoversi dalle sacche di compressione alle sacche di rarefazione, conservando la spinta della pressione iniziale. Questo causa il moto complessivo delle particelle in una specifica direzione. Chi osservasse il moto vedrebbe in pratica muoversi le sacche di compressione.

Il suono più fievole che l’orecchio può percepire (variazione di pressione di 20 µPa, ovvero 2^.10^-5 Pascal) è circa 5 miliardi di volte più debole della pressione atmosferica. I segnali sono rappresentati da piccole increspature che si sommano alla pressione atmosferica.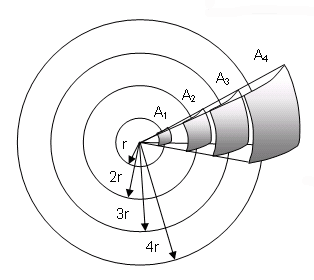

Nell’aria libera il suono si propaga uniformemente in tutte le direzioni, e la sua intensità diminuisce all’aumentare della distanza dalla sorgente. La stessa potenza sonora passa attraverso A₁, A₂, A₃, A₄, ma le aree aumentano proporzionalmente al quadrato del raggio. Questo significa che la potenza del suono per unità di area (intensità sonora) diminuisce proporzionalmente al quadrato del raggio.
La Legge dell’inverso del quadrato stabilisce che l’intensità del suono in campo libero è inversamente proporzionale al quadrato della distanza dalla sorgente. Se la distanza raddoppia, l’intensità si riduce a 1/4; se triplica, l’intensità si riduce a 1/9; se quadruplica, l’intensità si riduce a 1/16.

Nei prossimi tutorial sul suono ci occuperemo delle caratteristiche delle onde sonore: lunghezza d'onda, frequenza, fase, timbro. Inoltre studieremo il caso di onde complesse.

<< Indice