Quando si parla di audio è difficile non avere a che fare con i decibel; e quando si parla di decibel, è giocoforza avere a che fare con i logaritmi.
Per tutti quelli che non hanno la più pallida idea di cosa siano i logaritmi, perchè hanno studiato tutt'altro; per tutti quelli che non si ricordano un tubo e non hanno una gran voglia di andare a sfogliare vecchi libri di matematica alla ricerca di ciò che serve per comprendere cosa voglia mai dire che "il decibel è una grandezza logaritmica"... e anche per chi si ricorda quasi tutto ma "le proprietà no, tutte quelle formule non me le ricordo", questo breve tutorial spero possa costituire un semplice e chiaro strumento sufficiente per affrontare lo studio dei decibel.
Con un po' di rigore (è matematica, in effetti) ma anche senza inutili timori reverenziali, andiamo a vedere cosa abbiamo bisogno di sapere sui logaritmi.
Definizioni ed esempi
Per parlare dei logarimi, risaliamo un attimo indietro, e parliamo brevemente della funzione esponenziale, per quel poco che ci interessa sapere. A noi interessa infatti un caso particolare, e solo di questo ci occupiamo.
La funzione esponenziale è quella che, dato un numero fissato a, associa ad ogni numero x il numero ax.
Accidenti, questo già è complicato?
Niente paura, spieghiamo i concetti uno ad uno.
Per gli scopi sintetici che abbiamo qui, non starò a soffermarmi su cosa sia una funzione: ci basterà l'idea intuitiva di un qualcosa che ad ogni oggetto in un insieme ne associa un altro preso da un altro insieme.
Così ad esempio la funzione "età" associa ad ogni individuo il numero dei suoi anni, ad ogni auto il numero della targa, etc. Le funzioni che ci interessano qui, associano uno ed un solo oggetto, che per semplicità chiamerò "risultato", come nell'uso comune. Per cui, dato un oggetto nello scaffale di un supermercato, la funzione "prezzo" applicata a quell'oggetto mi restituirà con certezza un certo risultato - un valore numerico che chiameremo appunto "il prezzo" - assegnato a quell'oggetto.
Nel nostro caso, le funzioni di cui ci occupiamo associano un numero ad un altro numero, e questi numeri saranno numeri "reali": questo termine sta a signicare che oltre a numeri del tipo 1, 2, 10, 478, avremo anche i numeri del tipo 3/5, 67/117, 1/1237 (le cosiddette "frazioni") e anche numeri che non si possono esprimere ne' nell'uno ne' nell'altro modo, ossia numeri "irrazionali" (appunto perchè inesprimibili in un modo "razionale") che si presentano nella forma del noto numero
Detto questo, che per noi è sufficiente, andiamo ad occuparci della funzione esponenziale in una forma molto particolare: quella in cui il numero a è uguale a 10.
Avremo allora la funzione esponenziale in base dieci che è è quella che ad ogni numero x associa il numero 10x.
Notiamo che il numero x è un numero reale: cioè può essere un numero come 3 o 12 ma anche un numero frazionario o irrazionale.
Per cui, dato un x qualsiasi, il risultato della funzione esponenziale in base dieci applicata al numero x sarà 10x.
Quello che vediamo qui sotto è il grafico della funzione esponenziale in base 10.
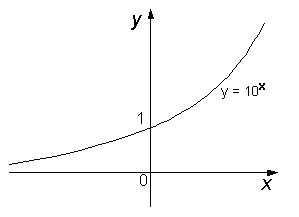
Perchè mi sono soffermato tanto sull'esponenziale?
E' semplice: perchè il logaritmo ne è esattamente l'inverso, ed il logaritmo in base dieci, che è quello utilizzato per definire i decibel, è esattamente l'inverso dell'esponenziale in base dieci.
Vediamo la definizione della funzione logaritmica: dato un numero reale positivo a diverso da 1, ed un numero non negativo x, esiste uno ed un solo numero y tale che ay = x. Tale numero si chiama logaritmo di x in base a e si indica col simbolo logax.
Complicato? Ma no! Pensiamoci su per un attimo. Il numero a diverso da 1, nel nostro caso è 10, perchè a noi interessa solo il logaritmo in base 10. Per cui andiamo a riscrivere l'intera definizione per la funzione logaritmo in base 10:
••• definizione •••
Dato un numero reale non negativo x, esiste uno ed un solo numero y tale che 10y = x. Tale numero si chiama logaritmo di x in base 10 e si indica col simbolo log10x, oppure semplicemente log x.
Quindi, quando cerchiamo il logaritmo in base dieci di un numero reale positivo - attenzione, questa è l'unica condizione - stiamo semplicemente cercando un numero che, dato come esponente a 10, ci dia come risultato proprio il numero di partenza.
Un paio di esempi semplici semplici.
••• esempio 1 •••
Vogliamo calcolare il logaritmo in base 10 del numero 100. Qual'è l'esponente da dare a 10 per ottenere come risultato il numero 100? Questo caso è piuttosto banale ed il risultato è 2: infatti 102 = 100.
Perciò scriveremo log 100 = 2.
Inoltre avremo nello stesso modo che log 1000 = 3 (infatti 103 = 1000), che log 10.000 = 4 (infatti 104 = 10.000) e così via: il logaritmo del numero 10...0 sarà uguale al numero di zeri dopo la cifra 1.
Per cui vediamo che l'andamento della funzione logaritmo è molto più lento di quello dei numeri reali: infatti ad 1 è associato il numero 0 (infatti 100 = 1, perchè qualsiasi numero elevato a 0 è uguale ad 1), a 10 il numero 2, a 100 il numero 3, a 1000 il numero 4: per arrivare ad associare il numero 100 abbiamo bisogno di applicare il logaritmo ad un numero con 100 zeri dopo la cifra 1!
Questo è quello che viene detto andamento logaritmico ed è ciò che caratterizza le grandezze come il decibel, ossia le grandezze che vengono calcolate mediante un logaritmo.
Quello che segue è il grafico della funzione logaritmo in base 10.
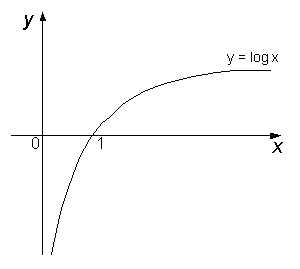
••• esempio 2 •••
Abbiamo visto come si calcolano i logaritmi in base 10 di numeri costituiti da un 1 seguito da più zeri. Ma come si calcola il logaritmo di un numero qualsiasi? Per esempio, come si calcola il logaritmo di 2354?
Ovviamente c'è un sistema, ma è molto complicato, e non ci interessa. Una volta si usavano le tavole logaritmiche, veri e propri volumi che riportano lunghi elenchi di logaritmi già calcolati, con l'uso dei quali è possibile calcolare tutti gli altri.
Noi invece utilizzeremo uno strumento meno affascinante e più veloce: la calcolatrice. Troppo semplice? Mi spiace per voi, se volete divertirvi procuratevi un vecchio volume di matematica.
Noi invece accendiamo la calcolatrice (o apriamo quella del pc) e ci domandiamo: qual'è il logaritmo in base 10 di 2354? Semplice: apro la mia calcolatrice scientifica, schiaccio il tasto "log", digito 2354, poi schiaccio il tasto "=", e leggo il risultato: 3,371806459. In genere basteranno le prime due, massimo tre cifre dopo la virgola, quindi possiamo arrotondare a 3,371 (diranno i più precisi: 3,372, il che è giusto).
Come vedete, il risultato 3,371 è compreso tra il numero 3, che è il risultato di log 1000, ed il numero 4, che è il risultato di log 10.000, il che è coerente col fatto che 1000 è minore di 2354 che è a sua volta minore di 10.000.
Questo fatto si esprime dicendo che la funzione logaritmo è continua e crescente.
••• esempio 3 •••
Resta un caso di cui occuparci: come si vede dal grafico, l'argomento del logaritmo può anche essere minore di 1.
Ho usato una parola che non ho spiegato: argomento. Che vorrà dire? Beh, l'avete capito da soli anche se non lo sapete: è il numero al quale applichiamo la funzione. Nell'esempio precedente l'argomento era 2354.
Abbiamo detto che l'argomento può essere inferiore a 1: ad esempio, 1/2. Oppure, 3/5. Cosa faremo? Niente di particolare: usiamo ancora la calcolatrice.
Se vogliamo calcolare log (1/2) facciamo prima 1 diviso 2 (che fa 0,5) e poi log 0,5 che fa -0,301 (arrotondato).
Notate che il risuiltato sarà negativo, ma questo dal grafico era evidente: i logaritmi di numeri inferiori a 1 sono negativi.
Proviamo con 3/5. 3 diviso 5 fa 0,6. Log 0,6 = - 0,22 (sempre con la calcolatrice, sempre arrotondato).
Proprietà
I logaritmi presentano delle proprietà particolari ed a loro modo divertenti, che facilitano i calcoli e sono particolarmente utili anche nei calcoli con i decibel.
Vediamo velocemente le più importanti.
••• prima proprietà •••
log (x * y) = log x + log y
Questa proprietà si esprime dicendo che "il logaritmo di un prodotto è uguale alla somma dei logaritmi dei fattori del prodotto" e vale anche per il prodotto di più fattori. Chi vuole può fare la fatica di dimostrarla: a noi qui non interessa, benchè la dimostrazione sia davvero semplice (basta la definizione di logaritmo e qualche semplice proprietà delle operazioni)
••• seconda proprietà •••
log xy = y * log x
Qui si ha che "il logaritmo di un numero reale x elevato ad un altro numero reale y è uguale ad y moltiplicato per il logaritmo di x". Per la dimostrazione vale quanto detto sopra.
••• terza proprietà •••
log (1/x) = - log x
Ovvero: "Il logaritmo dell'inverso del numero x è uguale all'opposto del logaritmo di x".
••• quarta proprietà •••
log (x/y) = log x - log y
Questa proprietà è una diretta conseguenza della prima e della terza proprietà, delle quali è in pratica una combinazione.
<< Indice